Overview

As shown in the video above, ECSE's collision detection system is continuous, allowing collisions to be detected even when objects are moving extremely fast. The system can detect a collision that occurs partway through a frame, and even allows object to react to that collision, potentially resulting in further collisions, before the frame has finished. Though the problem is somewhat complex, I solved it by building up from a number of relatively simple components.

Finding collision times

Before I delved into resolving collisions in a world with many objects, I first tackled the problem of detecting collisions between two objects. After some research into others' approaches, I made two key realizations:

1. The simplest way to represent the time at which a collision occurred is a floating-point number between 0 and 1, where 0 represents the current frame and 1 represents the next frame. I'll use this convention for the rest of this write-up.
2. It's much easier to find the time of collision between a moving object and a stationary object than it is between two moving objects. ECSE assumes that movement within a frame (i.e. the time scale of our collisions) is linear, so we can make use of this property this by subtracting the velocity of one object from both objects before we do our math. Effectively, this lets us deal with the relative velocity of one object as compared to the other, which is equivalent to a collision between a moving object and a stationary one.

Using this information, I started to write the collision detection functions. Note that ECSE supports circle colliders and line colliders, meaning we have three types of collisions we need to deal with (circle/circle, line/circle, and line/line). Line/line collisions are not yet implemented as they aren't currently being used in Magnaut, so I only cover the first two collision types here.

Detecting circle/circle collisions

I based my approach on an excellent Gamasutra article by Joe van den Heuvel and Miles Jackson. The article already describes the math in considerable detail, but I'll give a brief overview here ignoring several math tricks and optimizations for the sake of simplicity.

We have two circles centered at points A and B respectively. Before we even deal with velocity, we first check if the circles are already colliding by checking whether the distance between them is less than the sum of their radii. If so, the collision time is 0.

If not, we have to find whether they will collide this frame. Circle B is stationary, and circle A is moving with some velocity that will have it arrive at point A' by the end of the frame. We start by projecting the vector AB onto vector AA', which gives us C, the nearest point to circle B along circle A's trajectory. Of course, the point we actually want is D, which is the first point along circle A's trajectory at which the two circles are exactly touching.

To find point D, we can make use of the right-angled triangle formed by D, C, and B. We know the positions of C and B, so we can find the distance between them. The distance between B and D is just the sum of both circles' radii. Thus, using the Pythagorean theorem, we can calculate side DC of the triangle.

The position of D can now be found by subtracting DC from AC. The time of collision is given by the length of AD divided by the length of AA' (essentially the fraction of the circle's trajectory that it will cover before it hits the other circle).

Detecting circle/line collisions

Again, rather than reinventing the wheel, I based my approach on an article by Eric Leong, which I'll summarize here.

We have a circle centered at point A and moving toward point A', and a line segment which extends from point B to point C. We want to find point D, which is the first point along A's trajectory at which the circle's radius touches the line:

First, we project point A onto the line by projecting vector BA onto vector BC. This point (which we will call N) is the nearest point on the line to circle A:

If the distance between A and N is less than the circle's radius, then the entities are already colliding and the collision time is 0. Otherwise, we calculate the point of intersection between the line formed by AA' and the line formed by BC (note that we want to intersect with the lines, not just the line segments). This can be done a number of ways, but ultimately comes down to solving a linear system of equations describing the two lines, so I won't go over the details here.

If there is no point of intersection, the lines are parallel to each other, in which case we need to check if the circle collides with either of the line segment's endpoints. This can be done by doing a circle-circle collision check with the nearest endpoint to A, where the endpoint is a circle with radius 0.

If there is a point of intersection, then we need to find the point at which the circle will touch the line — the point of intersection we've found is only when the circle's center will touch the line, so we need to "back up" the circle a bit. We start by normalizing AN and projecting AA' onto it, which gives us the velocity of the circle towards the line (call this s). To exactly touch the line, the circle would need to move towards the line by the magnitude of vector AN minus the circle's radius (call the result of this calculation d). Therefore, the time at which the circle will collide with the line is s/d. If we multiply AA' by the collision time and add A, we can calculate D!

However, we've only found the time of collision between the circle and the line, not the circle and the line segment,so the circle may very well have collided with the line at a point past the line segment's endpoints. To check if the circle hit the segment, we project BD onto the BC, giving us P. If P is within the endpoints, then we've found the collision time with the line segment!

If P is past either of the endpoints, then the circle will not collide with the line segment; however, it may still collide with an endpoint. In this case, the problem reduces to a 0-radius circle/circle collision check as when the circle's velocity is parallel to the line. However, in this case, the check is between the circle and the nearest endpoint to P rather than the nearest endpoint to A.

Resolving collisions

At this point, I got basic collision detection working by simply checking every collider in the world against every other collider using the above two methods.

Optimization issues aside, I quickly realized that there was another problem: we can detect all of the collisions that will occur in a frame, but collisions often result in an object being destroyed or changing its trajectory, meaning subsequent collisions may not happen. For instance, in the example below, circle A may collide with both circles B and C, but if it stops moving at point A' as a result of its collision with B, then the collision with C should not occur:

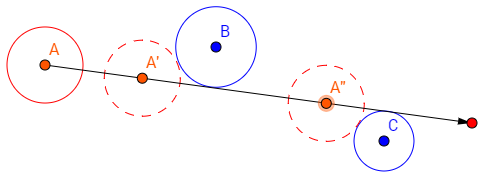
I solved this problem with the following algorithm:

1. Let startTime = 0.
2. Add every entity in the world to a list called changes.
3. Create a list of Collision structures that hold collision data for every pair of entities in the world (including the time of collision and pointers to both entities involved in the collision). Call this list potentialCollisions.
4. While changes is not empty...
   1. Run collision detection for every collision in potentialCollisions that involves an entity in changes. Update the corresponding Collision structures accordingly.
   2. Clear changes.
   3. Sort potentialCollisions by time of collision in ascending order.
   4. For each collision in potentialCollisions...
      1. Check if the collision time is greater than or equal to currentTime. If not, continue to the next item in the list.
      2. Notify function both entities involved in the collision. The entities return a list of entities that have had their trajectories changed as a result of the collision.
      3. If any changes occurred, add the changed entities to changes, set startTime to the time of this collision, and break out of this inner loop.

Effectively, we simulate inter-frame time so that entities are notified of collisions in order of when they would occur. This allows entities to respond to collisions as if they were being simulated in real time.

Potential improvements

Naturally, while continuous collision detection is far mroe accurate than discrete collision detection, it is also far more expensive. For Magnaut, I've found this system to be fast enough to cover my needs. However, there are a few optimizations that could be made. For instance, the algorithm currently checks collisions for every pair of entities in the world; instead, the world could be partitioned using a quadtree to reduce the number of collision checks.

Similarly, the ability to change an entity's trajectory in mid-frame may result in performance issues. For example, the bouncing ball demo above allows balls to continue rebounding an arbitrary number of times in a single frame until they have exhausted all of their movement speed, which can cause many collisions in a single frame.

On the one hand, this makes for a much more accurate simulation: if the balls had to "wait" until next frame before they could move again, then a very fast-moving ball may only move a small portion of its trajectory before coming to a stop for that frame, making its movement unrealistic and jerky.

On the other hand, if there are many balls or they're moving at very high speeds, collision detection can get very slow. In the worst-case scenario, if the entities' collision responses aren't carefully programmed, they could produce an infinite spiral of collisions that cause the engine to hang.

Ultimately, this is a tradeoff left up to the engine's user, as the algorithm is identical in either case: they can sacrifice speed for accuracy if they want to change trajectories mid-frame, or they can make their entities "wait" to move on the next frame for a simpler and computationally cheaper approach. Still, it may be possible to implement some cycle detection that makes it a bit harder for users to accidentally case a crash.