Overview

Splitting an object along the edges of a rectangular box (the shape of the portal in our game) is a complicated problem. To solve it, I decomposed it into smaller sub-problems, described below.

Our objects contain two essential components: a mesh renderer and a 2D polygon collider. Both of them need to be split in order for the object to function correctly. I decided that the first problem to solve was to write code to split both of these components along an arbitrary line.

Splitting a mesh on a line

I based this algorithm on the one outlined in this Stack Overflow answer. First, transform every point in the mesh such that the line we're splitting on is the y-axis. This makes it easier to reason about what we're splitting. We then create two empty meshes which will hold the two pieces resulting from the split.

For each triangle in the original mesh, we determine whether each vertex in the triangle is "left" (x < 0) or "right" (x >= 0). This gives us four cases: 1) every vertex is on the left, 2) every vertex is on the right, 3) one vertex is on the left and two are on the right, or 4) one vertex is on the right and two are on the left. In the first two cases, we just add the triangle to the mesh for the appropriate side. Otherwise, the triangle will be split by the line, so we need to do more geometry.

Assume for this example that there are two vertices on the left and one on the right. Let the vertices on the left be A and B, and let the vertex on the right side be C. Then let the point of intersection between the vector AC and the y-axis be D, and the point of intersection between the vector BC and the y-axis be E:

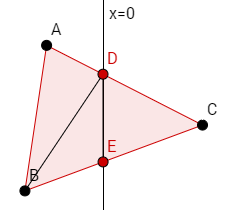
This gives us three new triangles: ADB, BDE, and DCE. ADB and BDE will go in the left side's mesh, and DCE will go in the right side's mesh.

Once we've iterated through every triangle in the original mesh, we transform all the vertices back to their real local positions (i.e. the inverse of the transformation we applied at the beginning). The mesh is now split!

Splitting a collider on a line

We used Unity's PolygonCollider2D collider for all of our objects, which are defined by an arbitrary number of closed paths. As with the mesh, we first transform the points so that the splitting line is the y-axis. We then apply the following splitting algorithm to each of the paths separately, so for each path in the original object, we have a left path and a right path.

To simplify the logic of this algorithm, I restricted our game to only use convex colliders. As a result, if we follow the path from point to point, it will either never cross the y-axis (meaning it's entirely on one side of the y-axis, so we can directly copy the path to that side's collider), or it will cross over exactly twice: once from left to right, and once from right to left. For instance, in the following diagram, we cross over on the edges BC and DA. Splitting along the y-axis, this would result in new points E and F, which form a new edge that is included in both paths.

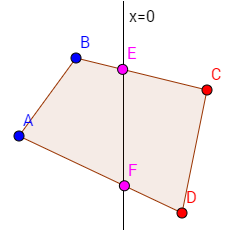
With that in mind, our algorithm for collider splitting is straightforward:

1. Create two new empty paths (leftPath and rightPath).
2. Determine whether we've started on the left or the right of the y-axis. (Assume for this example that we start on the left, but note that if we start on the right, we can just replace "left" with "right" in the following steps.)
3. Walk along the original path, adding each point to leftPath, until we reach a point on the right of the y-axis. Find the point of intersection between the y-axis and the edge between the previous point and the current point; add this point to both leftPath and rightPath.
4. Continue walking along the original path, but now add each point we encounter to rightPath instead.
5. Again, when we find an edge that crosses the y-axis, find the point of intersection and add it to both paths.
6. Continue walking along the original path, adding each point we encounter to leftPath, until we reach the end of the original path.

As with the mesh, we then transform these points back into local space. The collider is now split!

Splitting a composite object

As mentioned earlier, we required that all collider paths be convex to simplify the splitting algorithm. However, if we cut a corner out of an object, this would result in a concave collider. To work around the problem, we instead allowed splittable objects to made up of multiple colliders and meshes in child GameObjects, so what appears to be a concave shape can actually be made up of a group of convex shapes. As a result, when a single splittable object is being split, we may have to split several child objects.

To accomplish this, we clone the original object. The original object will become the "left" side of the split, and the clone will become the "right" side. Then, for each child of the left object, we attempt to split its mesh and its collider. If a split occurs, we update the corresponding child on both sides accordingly. If no split occurs, then the entire mesh/collider is on one side of the splitting plane, so we leave the child on that side as it is and delete the corresponding child on the other side.

If, after splitting all of the children, one of the sides has no children, we delete it entirely.

Splitting on a rectangle's edge

Now that we've solved the problem of splitting on a line, we can tackle the problem of splitting on the edges of an axis-aligned rectangle, which is the actual shape of our portal. This rectangular split can be decomposed into four line splits — one for each edge of the rectangle. Cutting along each of these lines results in 9 sections:

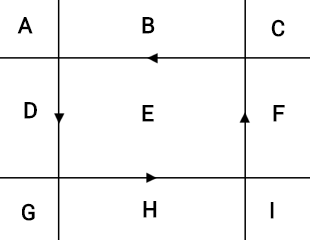
Section E will be transferred through the portal; all of the other sections form a rim around the rectangle and will need to be "glued" together into a single object (i.e. made children of the same parent object), as we don't actually want it split into 8 parts.

Rather than wrestling with bounding boxes and imprecise floating point math to determine which piece is in section E, we can instead wind the direction of the line cuts counter-clockwise around the circle (as shown by the arrowheads in the diagram). This way, section E is the only section that is "left" of every line cut. Keep in mind that in our composite object splitting algorithm, the "left" object is always the original object. This makes our algorithm very simple: cut the original object once for each of the lines, keeping a list of the newly-split "right" portions. If the original object hasn't been deleted (i.e. it still has children), it was on the left of every line and thus in section E, so transfer it through the portal. Finally, glue all of the other objects together.

Reducing hitching

We noticed during playtesting that if the portal cut many objects at once, there was a noticeable hitch due to the processing time required for this algorithm. I optimized the algorithm as much as I could using Unity's profiling tools, but despite making decent headway, I found that since the number of objects the player might be cutting at once is theoretically unbounded, no amount of optimization would truly solve the problem.

Instead, I used a trick to hide the processing time. I re-fitted the splitting functions in PortalManager as coroutines, which allow a function's execution to be temporarily suspended. At key points in the algorithm (primarly when an object is finished being split), we check to see if we've spent more than 10 ms of the current update step in the splitting algorithm. If we have, we suspend execution and resume it on the next update step. This allows us to continue rendering at the full frame rate while the splitting algorithm works away in the background.

Normally this would wreak havoc if objects were moving and being split at the same time. However, one of our game mechanics is that time freezes while the player is creating a portal, so we just keep time frozen until splitting is done. Even when cutting many objects at once, this is usually practically unnoticeable, taking only an extra frame or two to finish splitting. In extreme cases where processing takes a long time, it's still better than having the game completely freeze for the entire duration, as some animations and particle effects can continue while time is frozen.

Potential improvements

Ultimately, we felt that this algorithm was good enough in its current state, as we had limited time to implement it and it worked well for our purposes. However, given more time, there are two main things I would improve.

First of all, our "gluing" algorithm in the rectangle splitting step assumes that our object's overall shape is convex, which may not be true if the player cuts out part of the object (e.g. a "C" shape). This can result in two disconnected objects being glued together (e.g. if the player cuts only the right half of a "C" shape off, the "arms" of the shape will be glued together). In our experience, this case rarely comes up in gameplay unless the player intentionally tries to cause it, so we focused our limited development time on other problems. However, it could be resolved by checking whether pieces have any vertex locations in common before merging them.

Secondly, if splitting happens exactly at the edge of an object, we may produce empty objects or tiny "slivers" of the original object. This can happen when the player uses the undo button, as it redraws a portal at exactly the same location. Our workaround to the problem is just to check if each newly split object is below a certain size threshold and if it is, delete it. A better solution would handle this at the mesh/collider splitting stage, as we currently treat a point exactly on the y-axis as being right of the y-axis, though debugging this would unfortunately have taken more time than we had.